About the New Largest Prime Number
In this post I explain how the new largest prime number is found and their connection to perfect numbers, a 2500 year old math concept.
Introduction
In October 11 2024, a new largest prime has been found by Luke Durant and the Great Internet Mersenne Prime Search (GIMPS) project [1] [2]. The number is \(2^{136\,279\,841}-1\) and it has a whopping 41,024,320 digits. The previously known largest prime was also discovered by the same project. The number was \(2^{82\,589\,933}-1\), it had 24,862,048 digits, which is quite a bit smaller than this new one [1]. In this blog post, I explain the following:
- I start by explaining some theory related to prime numbers, what they are, and how we know there are an infinite number or prime numbers.
- I explain what the perfect numbers are, gradually working my way up to their relation with the so-called Mersenne primes.
- I explain why the new largest primes all have the form \(2^n-1\) (i.e, Mersenne primes), and how they are calculated, why their calculation is more efficient than other prime calculation algotihms.
Preliminaries: Prime Numbers
Most people know what prime numbers are. I will nevertheless give a definition of them. Prime numbers are natural numbers greater than 1 that is not a product of two smaller natural numbers [3]. First few prime numbers are 2, 3, 5, 7…
There is another important concept, being relatively prime. For two positive integers $m$ and $n$, they are called relatively prime if they have no common divisor greater than 1. For example, $15 = 3 \cdot 5$ and 28 = $2^2\cdot7$ are relatively prime, even though neither of them are prime by themselves.
Wikipedia says that the earlies evidence of people knowing about prime numbers dates to around 1550 BCE [3]. Euclid, around 300 BCE, had quite a bit to say about prime numbers in his monumental mathematical work, Elements. Probably the most important theorem Euclid proved regarding the primes is the following:
Theorem (Euclid): There are an infinite number of prime numbers.
Proof: Assume, to the contrary, that there are a finite number of prime numbers. Let them be \(p_1, p_2, \text{...} , p_n\). Note that this list contains all of the prime numbers (under our assumption that there are finitely many of them). The number \(p_1\cdot p_2 \cdot \text{...} \cdot p_n + 1\) is not divisible by any of these prime numbers. Hence, it must also be a prime. However, we assumed that the list contained all of the primes. Therefore, there are an infinite number of prime numbers.
Now we move on to another concept, the perfect numbers, which is first exposited by Euclid in his Elements. We will move on to reveal their connection with a certain class of prime numbers (also first given by Euclid, but we will go further then him on this point).
Perfect Numbers and Mersenne Primes
Before starting this topic, I would like to mention that Veritasium has a fantastic video on this topic. It explains quite a bit of the same theory I am about to explain, but I am planning to give more details and proofs for my statements, while the Veritasium video is more focused on the history.
Unlike prime numbers, not everyone knows what a perfect number is. A perfect number is a positive integer that is equal to the sum of its positive proper divisors. Let me immediately follow up with two examples. $6$ is a perfect number. Its positive divisors are $1$, $2$, $3$ and $6$. We exclude $6$ itself, because it is boring. We are left with \(6 = 1 + 2 + 3\). This condition makes $6$ a perfect number. In a similar way, \(28 = 1 + 2 + 4 + 7 + 14\). Hence, $28$ is also a perfect number.
In order to proceed forward it is important to introduce some notation and prove some intermediate results. We will first introduce the divisor function, \(\sigma(n)\), and prove a critical result.
Definition (Divisor Function) [5]: The sum of divisors is the function
\(\begin{equation} \sigma(n)=\sum_{d\vert n}d \end{equation}\)
Example: For those of you who are not familiar with the notation above, \(\sum_{d\vert n}d\) means summing all positive integers $d$ such that $d$ divides $n$. For example, \(\sigma(10) = 1 + 2 + 5 + 10 = 18\). Note that, if $n$ is a perfect number, \(\sigma(n)=2n\) is satisfied. This is going to be how we are going to detect perfect numbers. We now move on to prove a critical theorem about the divisor function:
Theorem (Commutativity) [5]: $\sigma(mn) = \sigma(m)\sigma(n)$ if $m$ and $n$ are relatively prime.
Proof: Let $m_1$, $m_2$, … , $m_k$ be the divisors of $m$ and $n_1$, $n_2$, … , $n_l$ be the divisors of $n$. Then, $\sigma(m) = m_1 + m_2 + … + m_k$ and $\sigma(n) = n_1 + n_2 + … + n_l$. Then, the product:
\(\begin{equation} \left(m_1 + m_2 + ... + m_k\right)\cdot\left(n_1 + n_2 + ... + n_l\right) \end{equation}\)
covers all the divisors of $m\cdot n$ provided that $m$ and $n$ are relatively prime.
It is not terribly important to understand this proof, but you should know that we will use this theorem in the next proof. Euclid, who is, in my opinion, the first mathematical genius, not only stated what the perfect numbers are, he gave a way to find some of them. The following is a 2300+ year old statement that still is the best way of finding perfect numbers using Mersenne primes:
Theorem (Euclid 2): If $2^n-1$ is a prime number (i.e, a Mersenne prime), then $N=2^{n-1}\left(2^n-1\right)$ is a perfect number.
Proof: We start by noting that $2^n-1$ and $2^{n-1}$ are relatively prime, since $2^n-1$ is assumed to be prime. Hence, the commutativity theorem holds. Furthermore, $\sigma\left(2^n-1\right) = 2^n$ since the divisors of a prime number are $1$ and itself. We have the following:
\(\begin{equation} \sigma\left(2^{n-1}\left(2^n-1\right)\right) = \sigma\left(2^{n-1}\right)\cdot\sigma\left(2^n-1\right) = \left(2^{n}-1\right)\cdot2^n \end{equation}\)
I used the fact that $\sigma\left(2^{n-1}\right) = \left(2^{n}-1\right)$. This is a well known identity, which you can check for yourself. Notice that, in $(3)$, \(\sigma(n)=2n\) is satisfied. Hence, we established that $N$ is a perfect number.
This is certainly a great result, but there is more. What we ideally want is the converse (or something like the converse, we will see) of this Euclid 2 theorem. Those of you who are not familiar with mathematical logic may struggle to understand this previous sentence. I will make a slight digression into logic and explain what the converse of a conditional statement is.
Generally, theorems are given in this form: if P, then Q. This is also the case in the Euclid 2 theorem. We can write this as $P \implies Q$ using symbolic logic. The truth table for this is the following:
| $P$ | $Q$ | $$P \implies Q$$ |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
The converse of the statement if P then Q is defined as if Q, then P, which is definitely not the same statement. Let us write it in symbolic logic and give its truth table:
| $P$ | $Q$ | $$Q \implies P$$ |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
As you can see, they differ in some rows. The converse (?) of this Euclid 2 theorem was proved first by Leonhard Euler nearly 2000 years after Euclid proved the original statement. This shows that the converse of a theorem, if it is true, may be significantly harder to prove:
Theorem (Euler): Every even perfect number $N$ can be written in the form $N=2^{n-1}\left(2^n-1\right)$, where $2^n-1$ is prime.
Proof: See [5].
I omitted the proof of this statement, since it is slightly complicated. The reference [5] gives several proofs for this theorem, including the original one by Euler.
And herein lies the importance of Mersenne primes. Combining the theorems of Euler and Euclid 2, we can state that Mersenne primes (primes that can be written as $2^n-1$) generate every even perfect number using the formula $2^{n-1}\left(2^n-1\right)$. Learned people usually state this fact in the following way: There exists a bijection (one-to-one correspondence) between Mersenne primes and even perfect numbers.
Those of you who are careful readers may have a question in there mind. Why do we say a bijection exists only with even perfect numbers? What about odd perfect numbers? This brings us to two unanswered (as of yet) questions in mathematics:
- Do odd perfect numbers exist?
- Are there an infinite amount of perfect numbers?
I think it is clear we didnt answer the first question in any capacity in this blog post. Neither have we shown the second statement. Indeed, if we have managed to show that there exists an infinite number of primes of form $2^n-1$, we would have solved the second question, since the Mersenne primes generate perfect numbers. However, no one has managed to show this yet.
Up to now, I explained some theory related to perfect numbers, which are not really relevant to the discovery of the largest prime. This section only exists to show that this new discovery also generates the largest known perfect number, which would have approximately 82,000,000 digits (Indeed, we do not need Euler’s contributions to make this statement, the Euclid 2 theorem is enough).
In the next section, I will change gears and explain the following:
- Preliminaries of computing (assignments and loops) and determining the efficiency of calculations (so-called Big-O notation) in a very informal way.
- Approaches to calculating general primes and their efficiency. Prime sieves.
- Mersenne primes and their calculation.
Preliminaries: Computing
In this informal introduction to computing, I will focus on two key concepts:
- variables, assignment
- loops
Variables & Assignment
Variables are symbols that hold integers. They differ from usual mathematics, where variables usually take any value in some set (for example, $x\in \mathbb{R}$ means that $x$ can take on values in the set $\mathbb{R}$). In computing, any variable at any time has a definite value. The symbol is just an abstraction for that value. Assignment refers to setting the value of the variable. Let’s see a concrete example:
1 2 3
x <- 3 x <- 5 x <- 3 * 5 + 7
We have 3 assignment operations in a row. The variable x is assigned to the value of 3 at first. Then, the value of x is set to 5 and finally we set it to 24.
In computing, it is sometimes useful to define collections of objects. These are referred to asarraysorlists. Giving an example:1 2
x <- [1, 2, 3] y <- x[0] + x[2]
We initialize x as a collection of 3 elements. In line 2, x[0] refers to the first object in this collection, namely, 1. Therefore, y is initialized to 1 + 3 = 4.
Loops
Loops are the heart of computing. They are used to make iterative calculations. Here is an example.
1 2 3 4
x <- 3 while x > 0 do x <- x - 1 endThis is the sort of computation which is what computation is all about. The indented statement,
x <- x - 1, is repeated while x>0. The indented statement reduces the value of x by 1. Thus, after 3 iterations, we will stop.
There is another type of loop. See the following example. \1 2 3 4
x <- 0 for item in [1, 2, 3] do x <- x + item end1 2 3 4 5
y <- 0 z <- [1, 2, 3] for item in z do y <- y + item endIn this loop, we set the variable
itemis initialized to the values in the collection[1, 2, 3]. In the first iteration, we haveitem=1, in the seconditem=2and so on. Each time, we set the value of x to be its old value plus the value of thisitemvariable. Hence, we will havex=6at the end. The bottom example is exactly the same thing as the top example.
After all that, we come to a more challenging part, which is computational efficiency. In the efficiency project, we are usually concerned with the size of our inputs. Lets start with two examples:
1
2
3
4
input: n, a positive integer
output: z, the sum of values up to n, i.e, 1+2+...+n
z <- (n * (n+1)) / 2
1
2
3
4
5
6
7
8
9
input: n, a positive integer
output: z, the sum of values up to n, i.e, 1+2+...+n
z <- 0
x <- 1
while x <= n do
z <- z + x
x <- x + 1
end
These two programs calculate exactly the same value for every value of the input, n. However, notice that, in the first one, we do one multiplication and one division, regardless of how big our input (n) is. In the second one, we do n iterations of the while loop. If we assume that the computer takes t seconds to calculate the sum, we will have to wait nt seconds to get our answer. Therefore, we can say that the first calculation is more efficient than the second one.
This gives rise to the notion of computational complexity. We write $O(1)$ for the efficiency of the first code, because the time for its calculation doesn’t depend on the size of the input. For the second one, we write $O(n)$ since the time it takes to complete the computation scales linearly with the size of our input. There are other time complexities such as $O(n^2)$, $O(n^3)$, $O(n\log{n})$ and so on.
Approaches to Calculate Prime Numbers
Lets try to imagine how we can compute if a number is prime or not. Lets see the most straightforward approach:
1
2
3
4
5
6
7
8
9
10
11
12
13
input: n, a positive integer
output: true, if n is prime. false, otherwise
x <- 1
while x < n do
if n % x == 0 begin
return false
end
x <- x + 1
end
return true
I used some symbols which I haven’t explained. First, the if statement executes the indented block if its statement is true. The statement here is n % x == 0, which evaluates to true if the remainder of the division n/x is equal to 0. There is also the symbol !=, which means not equal.
The computational complexity for this program is $O(n)$. We can do better and notice that we only need to check the remainders up to the square root of the input number, which would yield a complexity of $O(\sqrt n)$, which is quite a bit more efficient.
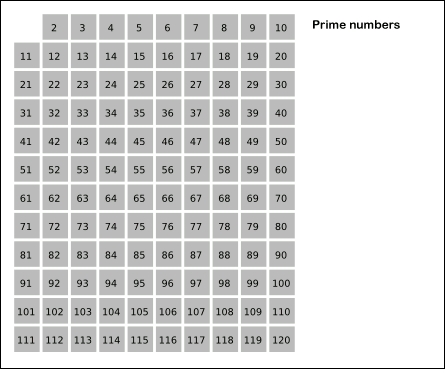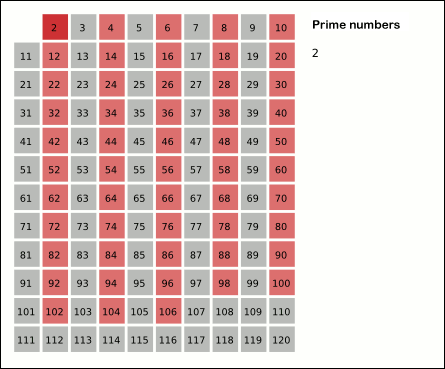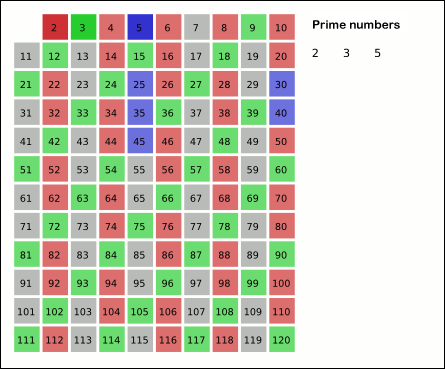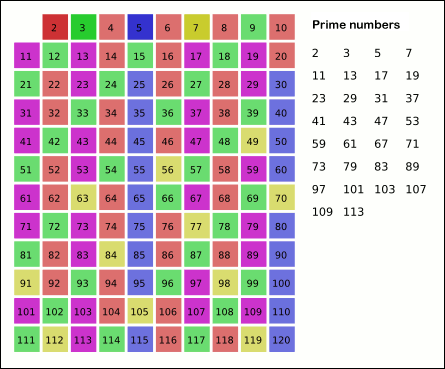
Lets ask a different question. How efficiently can we calculate what the prime numbers are in the first $n$ natural numbers. We can certainly check each one of the $n$ numbers using our $O(\sqrt n)$ program $n$ times, which yields a complexity of $O(n\sqrt n)$. There exists a better method, called the Sieve of Eratosthenes, invented by the Greeks circa 200s BCE [6]. I am not interested in explaining what this algorithm is in detail, which would be a large block of text. Instead, please view this gif image I found on Wikipedia [6].
Hopefully that makes it clear. This algorithm is said to have a complexity of $O(n\log\log n)$, which is quite a bit more efficient than our $O(n\sqrt n)$ algorithm. There are other, more complicated and slightly more efficient sieves out there, which are very much out of scope for this blog post.
Mersenne Primes and Their Calculation
So, what makes the calculation of Mersenne primes so much more efficient? The first step is to reduce the search space. With Mersenne primes, we are only iterating over the exponent $n$ (in $2^n-1$). Note that, in this newly discovered prime, the exponent is only 9 digits long, quite a bit less than the 41 million digit number it represents. Furthermore, there is another theorem, which we haven’t proved here, which states that if $2^n-1$ is a Mersenne prime, $n$ must also be a prime [7]. That further reduces the search space for $n$.
Afterwards comes the costly parts. After determining a prime $n$, we must check whether this $n$ generates a Mersenne prime. There is a very efficient way of checking whether a number divides a potential Mersenne prime, given under the Trial Factoring heading in the website [7]. In general, we can determine if a number $q$ is a factor of $2^p-1$ in logarithmic time using smart algorithms. Finally, we can take into account that any potential divisor of $2^n-1$ must be of the form $2kp+1$, another theorem which we haven’t proved here.
Unfortunately, none of these limitations allow us to check 42 million digit numbers. Instead, we look for a good while in order to be confident that we may have a prime, and check primality using the so called Lucas-Lehmer test, given below:
Theorem (Lucas-Lehmer Primality Testing) [7]: For $p > 2$, $2^p-1$ is prime if and only if $S_{p-2}$ is zero in the sequence: \(\begin{equation} S_0 = 4,\quad S_n = \left(S_{n-1}^2 - 2\right) \text{ mod } (2^p-1) \end{equation}\)
Proof: see [7]
Note that this theorem only requires us to calculate values up to the order of the exponent, which, again is only 9 digits long, and this calculation can be made. This is the last (and probably the most important) piece in the puzzle of prime number hunting.
Conclusion
Wow, this was quite a blog post. I hope you found it interesting and engaging. This blog post is my attempt at celebrating the work of the Great Internet Mersenne Prime Search project, which yielded the largest known prime number some days ago. I am planning to continue this blog if I have an interesting topic to talk about. I hope this blog post found you well. Cheers!
NOTE: There may be errors in this post, of which I am solely responsible. Please contact me if you detect any.
References
[1] https://en.wikipedia.org/wiki/Largest_known_prime_number
[2] https://www.mersenne.org/primes/?press=M136279841
[3] https://en.wikipedia.org/wiki/Prime_number
[4] https://en.wikipedia.org/wiki/Perfect_number
[5] https://jvoight.github.io/notes/perfelem-051015.pdf
[6] https://en.wikipedia.org/wiki/Sieve_of_Eratosthenes
[7] https://www.mersenne.org/various/math.php